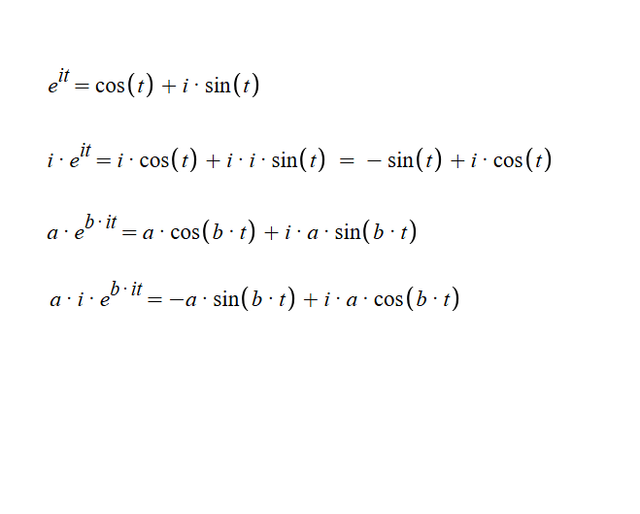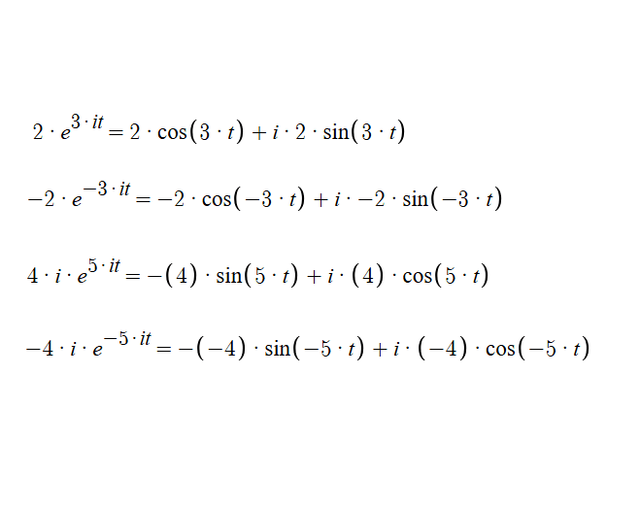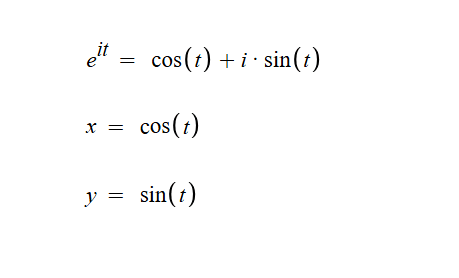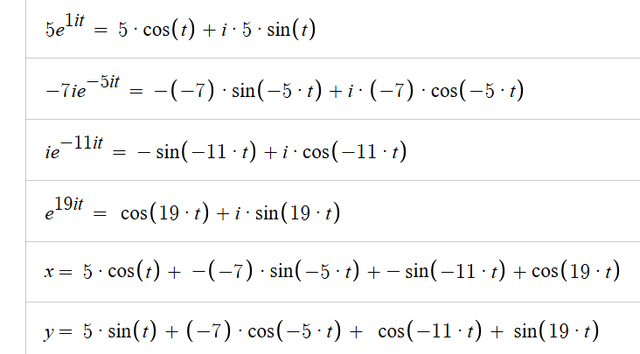LuaSTG로 복소수 곡선을 활용해서 다양한 탄막을 만드는 방법에 대한 글이에여
그리고 저도 잘 아는게 아니라 틀린 내용이 있을수도 있어요
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
마리사 탄막 모음집
youtu.be
이번 글에서 설명할건 위의 영상처럼 복소수의 곡선을 활용해서 다양한 탄막을 만드는 방법이에요
영상에 나온 레이저들이 모두 복소수의 곡선을 이용해서 만든 모양이에여
그리고 이 글에서 설명하는 내용은 위에 올려놓은 글에서 이어지는 내용이에여
1. 오일러의 공식
위에 올려놓은 그림이 오일러의 공식을 어떻게 전개하는지에 대한 방법이에요
맨 첫번째가 기본형이고 두번째줄이 앞에 i가 곱해졌을때의 전개방법이고
세번째 네번째는 앞이랑 제곱부분에 특정 값 a b 가 곱해졌을때의 전개방법이에요, 세번째가 기본형일때고 네번째가 앞에 i가 곱해졌을때에요
그리고 위에 올려놓은 그림이 첫번째 그림에서 설명한 방법대로 실제로 여러 형태의 오일러 공식을 전개하는 예시에요
첫번째는 a b 값이 곱해진 기본적인 형태고 두번째가 a b 값이 음수일 경우, 세번째는 i를 곱한 형태에 a b 값이 곱해진 경우고, 네번째가 i를 곱했을때 a b 값이 음수일 경우에 어떻게 전개되는지에 대한 예시에요
2. 복소수평면을 xy좌표평면으로 전환하기
복소수평면은 x축이 실수 부분이고 y축이 i가 곱해진 허수 부분인 평면이에요, 그래서 특정 복소수를 실수부분을 x좌표로 허수부분(i가 곱해진 부분)을 y좌표로 해서 복소수평면에 나타낼수 있어요
즉, 복소수평면을 기본적인 x y 좌표평면으로 전환하기 위해서는 복소수의 실수부분을 x좌표로, 허수부분을 곱해진 i를 빼고 y좌표로 넣으면 되요, 그리고 그게 위의 사진에 나와있는 설명이에요, 첫번째 오일러 공식인 복소수를 x y 좌표평면으로 옮기면 이때 그 x좌표는 두번째 줄처럼 되고 y좌표는 세번째 줄처럼 되요
여기서 cos sin은 각각 삼각함수고 t는 각도에요
3. 특정한 곡선의 공식을 x y 좌표평면으로 변환하기

그리고 앞에서 설명한 방식을 사용해서 오일러 공식의 형태로 나타내어진 특정한 곡선의 공식을, 즉 복소수의 형태로 나타내어진 특정한 곡선의 공식을 x y 좌표평면 위에서의 공식으로 전환할수 있어요
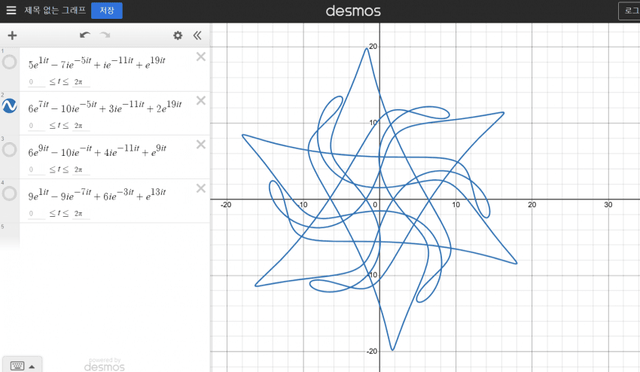
위의 첫번째 사진에서 왼쪽에 체크된 식이 오른쪽 곡선의 공식이에요, 그리고 그걸 실제로 전개해서 x y 좌표평면 위의 공식으로 변환하는 과정이 두번째 사진이에요
두번째 사진에서 첫번째 두번째 세번째 네번째 줄이 각각 공식의 첫번째 두번째 세번째 네번째 항을 전개한거고, 그것들을 모두 모아서 최종적으로 x y 좌표평면 위의 공식으로 전환한게 각각 x가 다섯번째 y가 여섯번째 줄이에요,
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
function complex_curve(a1,a11,a2,t)
if a11 == 0then
return a1*cos(a2*t), a1*sin(a2*t)
end
if a11 == 1then
return –1*a1*sin(a2*t), a1*cos(a2*t)
end
end
function complex_curve4(a1,a11,a2,b1,b11,b2,c1,c11,c2,d1,d11,d2,t)
x1,y1 = complex_curve(a1,a11,a2,t)
x2,y2 = complex_curve(b1,b11,b2,t)
x3,y3 = complex_curve(c1,c11,c2,t)
x4,y4 = complex_curve(d1,d11,d2,t)
return x1+x2+x3+x4,y1+y2+y3+y4
end
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
그리고 위에 올려놓은 코드가 이런식으로 복소수 곡선의 공식을 xy좌표평면 위의 공식으로 변환해주는 코드에요
첫번째 함수는 한개의 항을 변환해주는 함수고, 두번째 함수가 첫번째 함수를 활용해서 실제로 곡선의 공식을 변환해주는 함수에요, 실제로 탄막에서 사용되는건 두번째 함수에요
두번째 함수의 a1 a2에 각각 공식의 첫번째 항의 a값과 b값을 넣으면 되요, 맨 처음에 오일러 공식을 설명할때 나온 a값과 b값이에요, 그리고 a11에는 만약 i를 곱했다면 1 i가 없으면 0을 넣으면 되요
그리고 마찬가지로 b c d에는 각각 두번째 세번째 네번째 항의 값들을 넣으면 되요, 그리고 t에는 각도를 넣으면 되여



그리고 위에 올려놓은 사진이 영상에서 첫번째로 나오는 탄막의 코드에요, 첫번째 두번째 사진이 탄막의 코드고, 세번째가 발사하는 레이저랑 탄의 코드에요
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
function vector_turn(x,y,a)
return x*cos(a)-y*sin(a), x*sin(a)+y*cos(a)
end
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
이때 vector_turn함수는 위에 올려놓은 함수에요, 벡터의 회전공식을 사용해서 벡터 xy를 a만큼의 각도로 회전시켜주는 함수에요








그리고 위에 올려놓은 사진들이 영상의 나머지 탄막들에서 나오는 곡선들의 공식이에요,
역시 앞에서 설명한것과 동일한 방식으로 x y 좌표평면상의 공식으로 변환할수 있어요, 그리고 실제로 탄막을 생성하는 방식도 위에 올려놓은 탄막의 코드랑 동일한 방식이에요
그리고 이렇게하면 영상에 나오는것처럼 복소수 곡선들을 이용해서 탄막을 만들수 있어요
상하이앨리스환악단 갤러리
Copyright ⓒ 유머갤럭시 무단 전재 및 재배포 금지
본 콘텐츠는 뉴스픽 파트너스에서 공유된 콘텐츠입니다.